Future

Steps

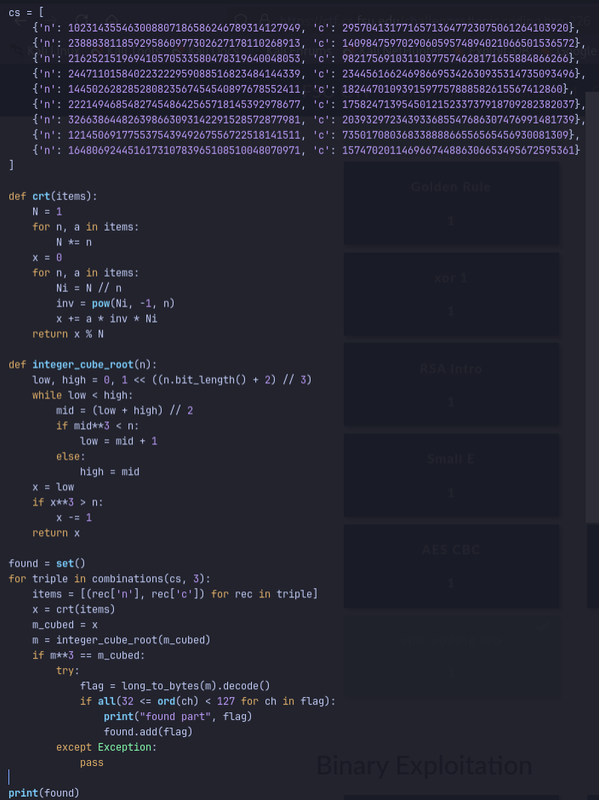
1. Collect all nine (n,c) pairs.
2. Write a script that does the following
3. Iterate over every combination of three pairs.
4. For each triple, use CRT to compute X≡c(mod n)
5. this yields X=m^3.
6. Compute the integer m=cuberoot(X) and check m^3=X
7. Convert m to bytes and verify it’s a printable flag.

---

Detailed Explanation (Including Screenshots)

For this problem we are given a future.zip file that when extracted gives two files: info.txt:
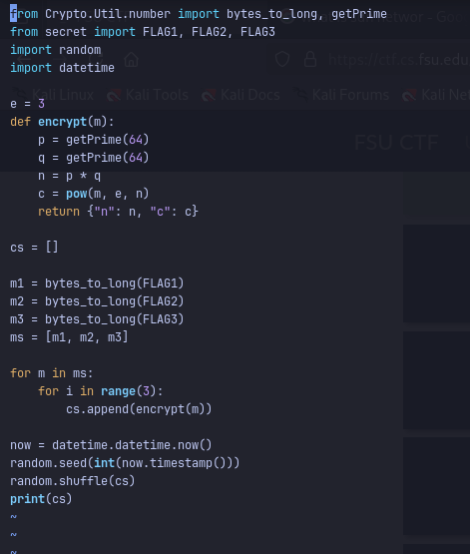
and enc.py:

From the looks of it this is a Chinese Remainder Theorem Problem:

The enc.py program encrypts 3 messages (3 parts of the flag) each 3 times under RSA with exponent e=3 and 64-bit primes for each encryption. The resulting nine ciphertexts (the ones in info.txt) are shuffled and released.

Each record is n = p*q and c = m^3 mod n

The same plaintext m was used for all three parts

We are given all 9 n, c pairs but we don’t know which triples belong together

When the same message is encrypted under three different n with exponent 3, if m^3 < n*n*n then we can recover m^3 by applying the CRT to the three.

x ≡c_i (mod n_i ),i=1,2,3 Since x = m^3 taking the integer cube root of x gives m (what we are trying to find)

However, since we don’t know which 3 correspond to a single flag, we must try all possibilities which is 9C3 = 84 possibilities.

To do this, I am going to write a script that:

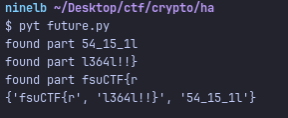
Loops through every combination of three n, c pairs out of the nine For each triple, It will compute x=CRT(n_i,c_i ) for i=1,2,3 Recover m by computing the cube root m = x^(1/3) Once we have m, it will convert it from its integer form using long_to_bytes from the Crypto library

It yields:

I rearranged the flag pieces to get: fsuCTF{r54_15_1ll364l!!} I submitted and verified the flag.