Real Shady Activities

Steps

1. Open info.txt
2. Observe it is an RSA problem
3. Find the q to part one by using FactorDB.com with the n
4. Use script that solves the encryption for part 1 of the flag
5. For part 2, find the p and q using the factorization of the n from FactorDB
6. Use the formula and script from part 1 to get the second half of the flag

---

Detailed Explanation (Including Screenshots)

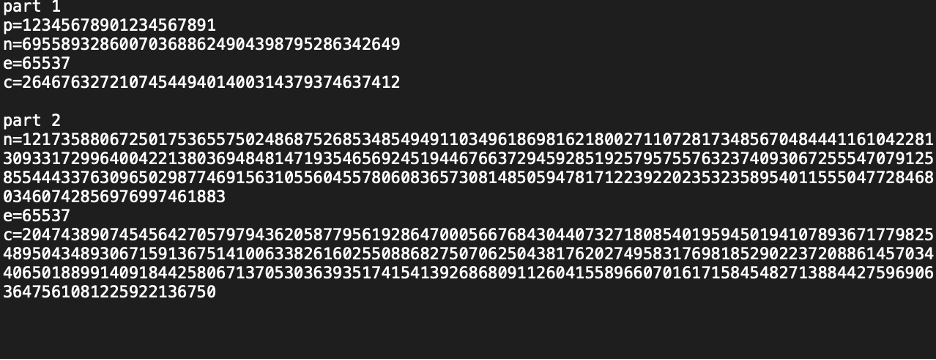
For this problem we are given a text document that has keys for an RSA encryption:

It is split into 2 parts, for part one we are given a p, n, e, and c value. We can use the n value to find the other factorization of it (q) on FactorDB:

Now that we have all the p, q, c, e, and n values, we can use the following script to solve for the plaintext:

from Crypto.Util.number import inverse, long_to_bytes

# Part 1 values
p = 11105580441296234919200907236291175908622846998665688502387374989234475099992221846069644422886733383699529058763023866081683746151428127719857074880731269
q = 10961685552231508042604181762271061333751942502162758663697754488945222725193681945116880210945532835675000224607261947873752437587973604689963482978347007
n = p * q
e = 65537
c = 79063544312984312798520911824890071392518809142618148822313633556824158262191049531006196303194865186500040421364473148533761705581532512148302648043423850857111233714713611143621575938326816556290765784453062375769346752272731913117638422743885325987599450917789833300609500761988030318812363483700646872529

phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))

When I run the script, I get the first part of the flag: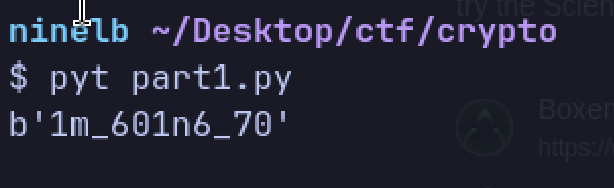

Now for the second part I need to get p and q to use the same method (Euler’s) to get the plaintext from the encryption. I am going to once again use FactorDB:

Yielding:

q = 10961685552231508042604181762271061333751942502162758663697754488945222725193681945116880210945532835675000224607261947873752437587973604689963482978347007
p = 11105580441296234919200907236291175908622846998665688502387374989234475099992221846069644422886733383699529058763023866081683746151428127719857074880731269

Then I run:

from Crypto.Util.number import inverse, long_to_bytes

# Part 2 values
p = 11105580441296234919200907236291175908622846998665688502387374989234475099992221846069644422886733383699529058763023866081683746151428127719857074880731269
q = 10961685552231508042604181762271061333751942502162758663697754488945222725193681945116880210945532835675000224607261947873752437587973604689963482978347007
n = p * q
e = 65537
c = 31918187411228991200206636803129347249461049156198289002174951103741795604040014098497097431502686392042251335475888630755521096032867001069089949048524654310477420603453217037486980308935810521707393843434371222232259086837508701025736041635736496922441249943404064734138264849151774706904073269398446931601

phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))